Lecture 1: The Geometry of Linear Equations
0. Intro
선형대수는 본질적으로 연립일차방정식의 Solution(해)를 구하는 학문이다.
일반적으로 연립방정식은 n개의 방정식에 n개의 변수가 주어지는데,
연립일차방정식을 바라보는 관점(Picture)에 따라 기하학적인 해석이 달라진다.
1. Row Picture
\[\begin{matrix} 2x - y = 0 \\\\ -x + 2y = 3 \end{matrix}\]먼저 2개의 방정식과 2개의 변수가 있는 연립방정식을 Row Picture(행의 관점)으로 해석해보자.
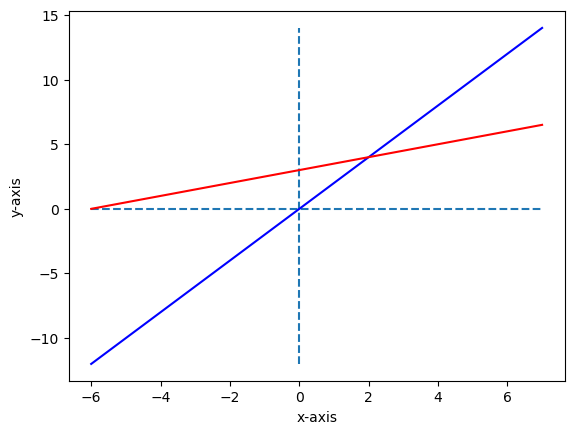
행의 관점에서 주어진 연립방정식의 해는 두 직선의 교점으로 볼 수 있다.
2. Column Picture
Column Picture(열의 관점)에서는 어떠할까. \[x \left[\begin{matrix} 2 \\ -1\end{matrix}\right] + y \left[\begin{matrix} -1 \\ 2\end{matrix}\right] = \left[\begin{matrix} 0 \\ 3\end{matrix}\right]\]
Column Vector(열 벡터)로 표현된 연립방정식을 그래프로 나타내보자.
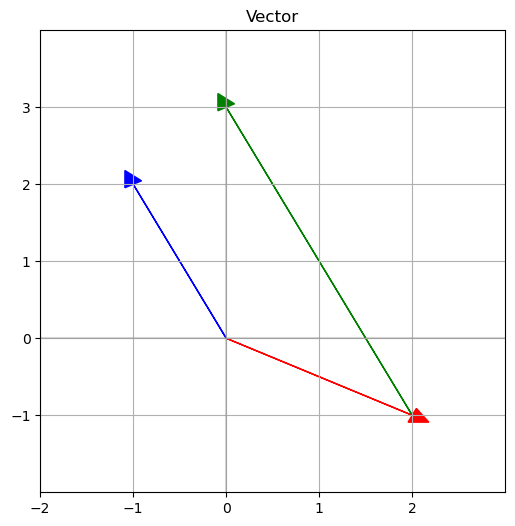
열의 관점에서 연립방정식은 열 벡터의 Linear Combination(선형 결합)을 찾는 문제로 바뀐다.
3개의 방정식과 3개의 변수가 주어진 연립방정식에서는 어떻게 될까?
3. Pictures in 3-dim
3-1. Row Picture
\[\begin{matrix} 2x-y=0 \\ -x+2y-z=-1 \\ -3y+4z=4x \end{matrix}\]위와 같이 3개의 방정식과 3개의 변수를 가진 일차연립방정식을 Row Picture로 해석해보자.
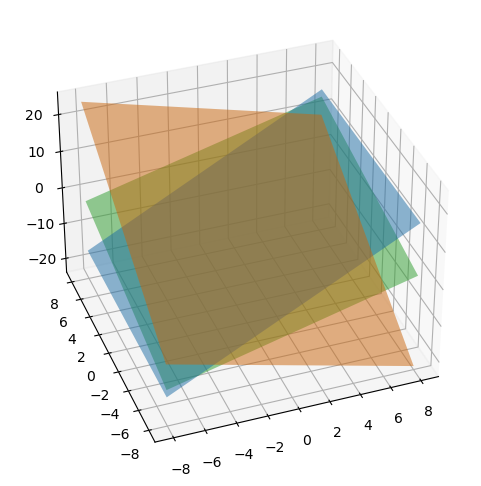
3차원에서는 평면끼리의 intersection으로 바뀌었다. Row Picture는 차원이 올라갈수록 직관적으로 이해하기 힘들다.
특정 도형들의 intersection이라는 점은 변하지 않지만 머리 속으로 상황을 이미지화하는게 어렵기 때문이다.
3-2. Column Picture
\[x\left[\begin{matrix} 2 \\ -1 \\ 0 \end{matrix}\right] + y\left[\begin{matrix} -1 \\ 2 \\ -3\end{matrix}\right] +z\left[\begin{matrix} 0 \\ -1 \\ 4\end{matrix}\right]= \left[\begin{matrix} 0 \\ -1 \\ 4\end{matrix}\right]\]연립방정식을 Column Picture로 해석하면, 3차원 벡터를 계수로 가지는 1차 방정식으로 볼 수 있다.
즉, 2차원과 동일하게 열 벡터들의 선형 결합을 찾는 문제로 이해할 수 있다. 열 벡터가 속한 차원만 바뀐 것이다.
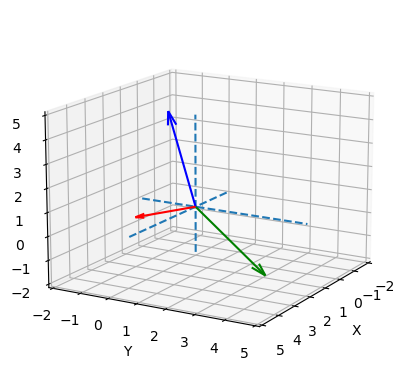
벡터의 선형 결합은 벡터가 속한 차원과 무관하게 동일한 이미지로 떠오르기 때문에 직관적으로 이해하기 편하다.
연립방정식을 방정식들의 intersection이 아니라 열 벡터의 선형결합으로 보면 이득인 부분 요약
4. Matrix Form
\[x\begin{bmatrix} 2 \\ -1 \\ 0 \end{bmatrix} + y \begin{bmatrix} -1 \\ 2 \\ -3\end{bmatrix} +z\begin{bmatrix} 0 \\ -1 \\ 4\end{bmatrix}= \begin{bmatrix} 0 \\ -1 \\ 4\end{bmatrix} \Longrightarrow AX = b\] \[A=\begin{bmatrix} 2 && -1 && 0 \\ -1 && 2 && -1 \\ 0 && -3 && 4\end{bmatrix} , \quad X=\begin{bmatrix}x \\ y \\ z\end{bmatrix}, \quad b= \begin{bmatrix}0 \\ -1 \\ 4\end{bmatrix}\]연립방정식을 다음과 같이 행렬식으로 나타냈을 때, 우변 b는 열 벡터의 조합으로 만들어야 하는 목표 지점(또는 벡터)가 된다.
여기서 행렬 A는 그대로 두고, b의 값을 바꾸면 어떻게 될지 생각해보자. 임의의 b에 대해 연립방정식 AX=b는 해를 가질까?
바꿔 말하면, 열 벡터들의 선형 결합으로 열 벡터가 속한 공간의 모든 점(point)들을 표현할 수 있을까?
이 질문에 대한 답이 Yes라면 행렬 A를 non-singular하다고 한다.
행렬 A가 Non-singular하다는게 무슨 의미이고 어떤 정보를 주는지 다음 수업을 통해 알아보자.
